

In this case we also say that the value of the limit is the value of the improper integral. The improper integral is said to converge if there exists the finite limit. Improper integrals with infinite limits of integration Various comparison arguments are of great help.Ĭomparison test: Let both functions and are unbounded at and for all.
#Improperintegrals notea series
As it was the case with infinite series also here the problem of convergence is easier to answer as the problem of finding the values to which the given improper integral converges. As the terminology convergent or divergent indicates there are close connections between the theory of improper integrals and infinite series. Often it is difficult to find the corresponding antiderivative which is necessary to answer the divergence of convergence of the given improper integral using the definition.

Provided both improper integrals on the right-hand side exist.
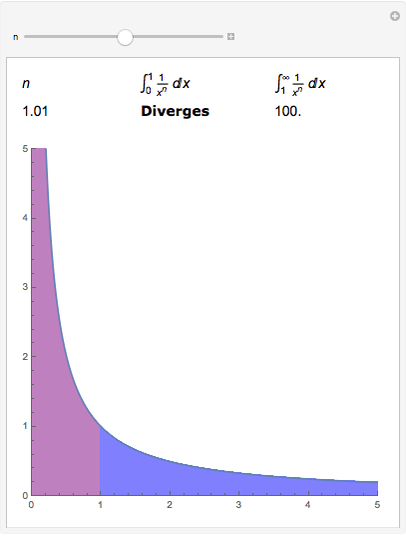
Similarly, when the integrand has improper one-sided limits at an inner point of interval but the integrand is defined on, then An analogous definition can be formulated when the integrand is unbounded at the lower limit of the integration. If the limit above does not exist or is improper we say that the improper integral diverges. If this holds we say that the value of the limit is the value of the improper integral. The improper integral is said to converge if the limit exists and is finite. Let and function be unbounded as approaches (from the left). Improper integrals with unbounded integrands


 0 kommentar(er)
0 kommentar(er)
